 |
|
 |
| About |
|
The motivation to build this site
can be traced back to early 1983 when
Cantor’s ternary function was introduced in
Douglas Lind’s
undergrad analysis sequence (MATH 424, 425, 426) at the
University of Washington. (Aside: I prefer the
quarter system,
which the UW still uses.) An inquisitive student named Peter asked about the values of its derivative on the
Cantor set.
Claiming to not know the answer, Lind posed it as a problem to the class.
He had previously given us “lollipop” problems—an actual
lollipop went to the author of the winning solution.
This time we were evidently ready for a taste more powerful than sugar, for he suggested letting
intellectual curiosity be our sole motivating force.
Applying knowledge from Ralph Greenberg’s number theory course (MATH 414), I proved that the derivative is positive infinity on a certain subset of the Cantor set. After reading my proof, Lind posed this follow‑up: With respect to the standard
coin-flipping measure,
does the Cantor function have infinite derivative almost everywhere
on the Cantor set?
This appeared to call for knowledge from Ronald Pyke’s probability sequence (MATH 394, 395, 396), except we didn’t cover any measure theory in that course. We hadn’t covered Lebesgue integration in Lind’s class yet either. I showed Professor Pyke my proof. After taking a few seconds to think about the follow‑up, he concluded that the answer is “yes” by the strong law of large numbers. He sketched out an argument and suggested I write up a full proof to send to the American Mathematical Monthly as a problem proposal. The idea of publishing mathematical work had never occurred to me, so this sounded really exciting. However, when I told Professor Lind about sending the problem to the Monthly, his response was less than enthusiastic. The following title might explain why. 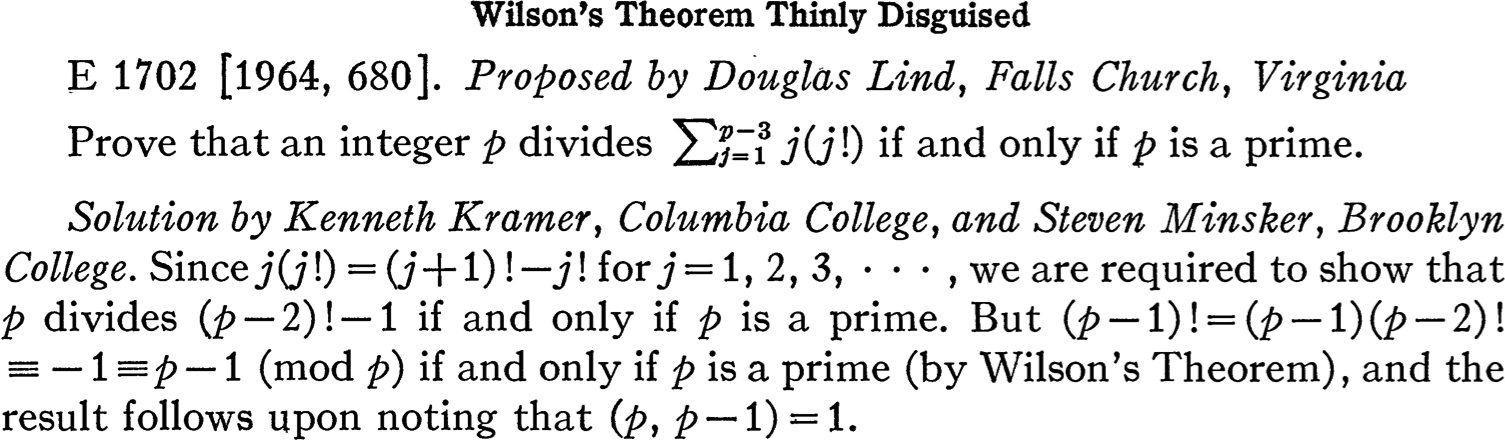
This was Lind’s first Monthly problem. He was still in high school when he proposed it. If he suspected or knew that his follow-up problem was just another well-known theorem “thinly disguised,” he would have been correct. 
Actually, the only thing that was disguised in this case was my institution, which the Monthly got wrong. Here is my second Monthly problem [1997 BRR PMark Bowron, Stanley Rabinowitz, Closure, Complement, and Arbitrary Union, Problem 10577, Amer. Math. Monthly, v. 104 no. 2, 1997, p. 169, Solution: John Rickard, v. 105 no. 3, 1998, pp. 282‑283.], co-proposed with Stanley Rabinowitz in 1997. 
When we proposed this, neither of us was aware that multiple solutions had already appeared in print. A list is posted here. The unoriginality of my first two problem proposals is what led me to gather and post a comprehensive list of references on the Kuratowski closure-complement theorem. The primary goal of this website is to help authors and editors avoid republishing old results. |
| mathematrucker 9 Jun 2019 |
